Абсолютной максимальной температурой является температура планка

Планковская эпоха

С именем Планка связаны многие величины и законы. В частности, физическая космология называет его именем эпоху самого раннего периода истории наблюдаемой нами Вселенной. Этот непродолжительный период, по теоретическим предположениям, продолжался в течение планковского времени, имеющего значение от 0 до 10-43секунд. В эту эпоху – около 13,8 млрд. лет назад – всё вещество Вселенной обладало энергией порядка 1019 ГэВ и было сосредоточено в одной точке. Радиус этой точки имел значение ~10−35 м, плотность ~1097 кг/м3, а температура ~1032 К. Поскольку размеры Вселенной были исключительно малы, случилось преобладание квантовых эффектов гравитации над физическими взаимодействиями. Невероятные значения температуры и плотности делали вещество неустойчивым. Произошло нарушение симметрии, что привело к проявлению фундаментальных сил – гравитационное воздействие отделилось от других фундаментальных взаимодействий.

Преимущества планки

Выполняя планку, мы можем рассчитывать на ряд преимуществ. А именно:

Формирование фигуры, за счет укрепления мышц пресса. Выполнение планки подтянет живот, и он не будет выпирать. Сделав талию более плоской.
Укрепляются мышцы спины. Это снижает риск получения травм в области поясницы.
Повышается выносливость всех работающих мышц. Это сделает тренировки более интенсивными.
Улучшается осанка. И визуально наши плечи кажутся более широкими, а мы будем выглядеть более атлетично.
Укрепление суставов. Что позволит снизить риск получения травм во время тренировок в зале, с большими весами.
Планку можно выполнять не только в тренажерном зале. Поэтому она отлично подойдет для атлетов, тренирующихся дома.
Улучшается концентрация. Планка требует собранности

Во-первых, мы должны концентрировать внимание на том, чтобы тело было ровным на протяжении всего выполнения. Во-вторых, обязательно надо следить за дыханием

Оно должно быть ровным. Никаких задержек.
Выполнение планки помогает расслабить мышцы. Поэтому его рекомендуют выполнять в конце тренировки. 
Как утверждают йоги. Если тело расслабленно и в мышцах отсутствуют зажимы. Ваш ум успокаивается, а мысли становятся более ясными. Не знаю так это или нет. Но вряд ли бы, йоги просто так стали это утверждать.
Выполнение планки, возбуждает симпатическую нервную систему. Она подготавливает наш организм к тяжелой работе. Ускоряя сердцебиение и насыщая мышцы кровью.

Всего лишь одно упражнение, может принести такую пользу. 

Конечно же, не все так гладко как кажется. Для новичка, который до этого не занимался атлетизмом или вообще каким-то спортом. Выполнение планки будет даваться очень трудно. То же самое касается и людей с излишним весом. Даже йоги рекомендуют в начале изучить более легкие позы, прежде чем приступать к этой. Также не стоит приступать к выполнению планки, если у вас имеется травма позвоночника. Хоть врачи иногда и рекомендуют данное упражнение в реабилитационных целях. Все же стоит быть предельно осторожным при его выполнении.

Литература

• Massieu F. Sur les fonctions caractéristiques des divers fluides (фр.) // Comptes Rendus de l’Académie des Sciences, 1869, vol. 69, pp. 858–862.
• Massieu F. Addition au précédent mémoire sur les fonctions caractéristiques (фр.) // Comptes Rendus de l’Académie des Sciences, 1869, vol. 69, pp. 1057–1061.
• Massieu F. Mémoire sur les fonctions caractéristiques des divers fluides et sur la théorie des vapeurs (фр.) // Memoires présentés par divers savants étrangers à l’Académie des Sciences de l’Institut National de France, 1876, vol. 22, pp. 1–92.
• Münster A. Statistische Thermodynamik. — Berlin — Göttingen — Heidelberg: Springer-Verlag, 1956. — XII + 852 p.
• Базаров И. П. Термодинамика. — М.: Физматгиз, 1961. — 292 с.
• Базаров И. П. Термодинамика. — 5-е изд. — СПб. — М. — Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
• Барилович B. A., Смирнов Ю. А. Основы технической термодинамики и теории тепло- и массообмена. — М.: ИНФРА-М, 2014. — 432 с. — (Высшее образование: Бакалавриат). — ISBN 978-5-16-005771-2.
• Белоконь Н. И. Термодинамика. — М.: Госэнергоиздат, 1954. — 416 с.
• Биккин Х. М., Ляпилин И. И. Неравновесная термодинамика и физическая кинетика / Науч. ред. В. В. Меньшенин. — Екатеринбург: УрО РАН, 2009. — 500 с. — (Физика конденсированных сред. Т. 1). — ISBN 978-5-7691-2034-3.
• Герасимов Я. И., Древинг В. П., Еремин Е. Н. и др. Курс физической химии / Под общ. ред. Я. И. Герасимова. — 2-е изд. — М.: Химия, 1970. — Т. 1. — 592 с.
• Гиббс Дж. В. Термодинамика. Статистическая механика / Отв. ред. Д. Н. Зубарев. — М.: Наука, 1982. — 584 с. — (Классики науки).
• Гиббс Дж. В. Термодинамические работы / Пер. с англ. под ред. проф. В. К. Семенченко. — М. — Л.: Гостехтеориздат, 1950. — 492 с. — (Классики естествознания).
• Глазов В. М. Основы физической химии. — М: Высшая школа, 1981. — 456 с.
• Зубарев Д. Н., Морозов В. Г., Рёпке Г. Статистическая механика неравновесных процессов / Пер. с англ. под ред. В. Г. Морозова. — М.: ФИЗМАТЛИТ, 2002. — Т. 1. — 432 с. — ISBN 5-9221-0211-7.
• Кричевский И. Р. Понятия и основы термодинамики. — 2-е изд., пересмотр. и доп. — М.: Химия, 1970. — 440 с.
• Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
• Мюнстер А. Химическая термодинамика. — М.: Мир, 1971. — 296 с.
• Николаев Г. П., Лойко А. Э. Техническая термодинамика. — Екатеринбург: УрФУ, 2013. — 227 с.
• Патров Б. В., Сладков И. Б. Физическая химия. Ч. 1. — СПб: Изд-во Политехн. ун-та, 2009. — 127 с.
• Полторак О. М. Лекции по химической термодинамике. — М.: Высшая школа, 1971. — 256 с.
• Полторак О. М. Термодинамика в физической химии. — М.: Высшая школа, 1991. — 320 с. — ISBN 5-06-002041-Х.
• Семенченко В. К. Джосиа Виллард Гиббс (рус.) // Гиббс Дж. В. Термодинамические работы. — М.: Гостехиздат, 1950, с. 12—23.
• Серафимов Л. А., Фролкова А. К., Хахин Л. А. Правило фаз. — М.: МИТХТ, 2008. — 48 с.
• Сычев В. В. Дифференциальные уравнения термодинамики. — 2-е изд., перераб. — М.: Высшая школа, 1991. — 224 с. — ISBN 5-06-002071-1.
• Сычёв В. В. Дифференциальные уравнения термодинамики. — 3-е изд. — М.: Изд-во МЭИ, 2010. — 256 с. — ISBN 978-5-383-00584-2.
• Сычев В. В. Сложные термодинамические системы. — 4-е изд., перераб. и доп.. — М.: Энергоатомиздат, 1986. — 208 с.
• Сычёв В. В. Сложные термодинамические системы. — 5-е изд., перераб. и доп.. — М: Издательский дом МЭИ, 2009. — 296 с. — ISBN 978-5-383-00418-0..
• Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин. Сборник определений / Комитет научно-технической терминологии АН СССР. — Вып. 103. — М.: Наука, 1984.
• Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — Т. 5: Стробоскопические приборы — Яркость. — 760 с. — ISBN 5-85270-101-7.
• Хачкурузов Г. А. Основы общей и химической термодинамики. — М.: Высшая школа, 1979. — 268 с.

Планковские чёрные дыры

Этот тип чёрной дыры пока гипотетичен, но если они существуют, минимальная масса их должна быть равна планковской массе. Этот объект соответствует предполагаемому максимону, частице с такой же массой. Вероятно, что эта гипотетическая чёрная дыра – конечный продукт жизни обычной чёрной дыры. Она должна быть стабильна и не иметь излучения Хокинга. Плотность такого объекта будет выражаться значением порядка 1094 кг/м3 . Такие масштабы физики станет описывать квантовая гравитация, если учёные смогут разработать надлежащие теории.

На границе XX и XXI веков началась революция перехода метрологии в квантовую стадию. Она не в полном объёме основана на планковской системе, но всё-таки стоит на её фундаменте. Именно планковские единицы являются определяющими для применения современных физических теорий. Вдумываясь в значения планковских величин, невольно пытаешься представить эти невероятные массы и расстояния, плотности и время. Это очень сложно, практически нереально, но желание проникнуть в тайны природы всегда озаряло человеческую мысль…

Пока квартир хватит

Впрочем, на ближайшие несколько лет запаса квартир хватит. «В ближайшей перспективе снижение количества выданных разрешений не скажется на рынке никак. Выданные ранее разрешения на строительство предполагают разную периодичность, разный срок реализации проектов, возможность реализации их по этапам на перспективу в несколько лет. Поэтому рынок будет насыщен проектами, на которые уже получена исходно–разрешительная документация», — говорит Екатерина Тейдер, директор направления девелопмента Becar Asset Management. «Но в дальнейшем это приведет к дефициту объема предложения и росту цен, что отразится на снижении спроса. Предпосылки этого мы сможем увидеть уже во второй половине текущего года, однако ярко выраженные черты они приобретут к 2020 году», — прогнозирует Ольга Ульянова, директор департамента рекламы и маркетинга ГК «Полис Групп».

Насколько подорожает из–за грядущего дефицита стройка — пока неясно. «Сейчас можно предполагать, что по итогам перехода на эскроу–счета себестоимость строительства только за счет банковского сопровождения вырастет на 7–12%. Поэтому можно предполагать, что конечная цена к концу 2019 года станет больше на 5–10%», — говорит Роман Мирошников, исполнительный директор СК «Ойкумена».

Кроме того, по мнению экспертов, рынок покинут компании, не имеющие собственных средств на строительство и не сумевшие получить проектное финансирование от банков. Остальные девелоперы будут учиться балансировать между получением дохода от своей деятельности и поддержанием платежеспособного спроса. «Себестоимость строительства вырастет за счет инфляции, увеличения налогового бремени и перехода на проектное финансирование с использованием системы эскроу–счетов. На получение банковского кредита потребуется больше трудозатрат, поэтому каждый проект будет тщательно анализироваться на предмет доходности и востребованности на рынке», — говорит Ася Левнева. «Конкуренция велика, и ни один застройщик не может диктовать свою позицию рынку строящегося жилья. На цену влияют другие факторы — в первую очередь степень готовности жилого комплекса, наличие спроса на него», — считает Сергей Терентьев, директор департамента недвижимости ГК «ЦДС».

Сегодня очевидно, что торопиться получать разрешения не имело смысла. Все проекты, независимо от даты получения разрешения, должны с 1 июля перейти на счета эскроу. Исключения могут быть сделаны для объектов со степенью строительной готовности 30% и с объемом заключенных ДДУ не менее 10% от общей площади помещений. При этом произошло некоторое накопление разрешений на строительство, которые теперь будут реализовываться без излишней поспешности. Вероятно, в ближайшее время застройщики будут работать в обычном режиме, адаптируясь к законодательным изменениям. К работе с проектным финансированием и счетами эскроу должны будут приспособиться все участники рынка, в том числе банки и покупатели.

Юлия Ружицкая

Директор по продажам «Главстрой Санкт–Петербург»

В прошлом году активность застройщиков по расширению портфеля проектов на начальных стадиях была очень высока. Это было заметно и по скачку спроса на земельные участки, и по росту количества выданных разрешений на строительство. Таким образом, еще в 2018 году девелоперы сделали стратегический запас готового к выводу на рынок предложения. Этого должно хватить на период становления новой схемы работы по эскроу–счетам.

Игорь Креславский

председатель правления ГК «РосСтройИнвест»

Путь к изменению определения килограмма

значению CODATA постоянной ПланкаУильям Фрэнсис МэджиАнри ПуанкареНаука и МетодВалентина БергманаЖана-Мари Суриовторой когомологической группы алгебры Ли группы ГалилеяХансом РейхенбахомКарлом Фридрихом фон ВайцзеккеромПаскуаль Йорданконденсированных средЭренфестПаулиЛандаулюбимый примерстепенном законе хищника-жертвыТексье и др.speed_maxlnmassработ Бендераместом для объединения памятников всех наук и искусствДжокондуминиатюрные реплики килограммаэлектронномукилограмму12nm12nEmc2-10легко обнаруженасовременного масс-компаратораm12Cum12Cuпоследнее сравнение использования различных наборов констант для определения килограммаПереопределение килограмма: решение, время которого пришлоMetrologiaНовые поступления,Определения, которые фиксируют значение постоянной Планка hТрактате об электричестве и магнетизмеФранцЭдуард ЗахерыEmc2Ehfmmhfс2hс,mКомптонНильс БорEmc2ΔmΔth/с2Розенфельд-52mfmс2h50экспериментыЛуи де Бройльhhh-8hμ-8-8О законе распределения энергии в нормальном спектреhbh):h,кhHilfsgrösseвозможнодействительно не помнитРеймонд Тайер Бирге опубликовал первое детальное сравнение-34-34удивительный прогрессhhэту статьюБрайана недавняяверсия LEGOизменилась ли его массапроект АвогадроN_АhN_Аhh-11снова синхронизированаВладимира Арнольдасимплектического верблюдаВернер Гейзенбергстатью Бродского-Хойерħпостоянной Планка в классической механикеhОн был поражен15 лет назадсубпланковские структурыЮджин Вигнерфункции Вигнераквантовых ковровхрhhбланк CODATAhhздесьплатинаÀ tous les temps, à tous les peuples!

Техника выполнения упражнения планка

Поначалу может показаться, что планка – упражнение легкое, но это не так. Не каждому человеку удается вначале продержаться более 30 секунд. Основная задача выполнения упражнения планка – совокупное напряжение мышц кора при удерживании своего тела на локтях и на пальцах ног. Последовательность выполнения упражнения включает несколько шагов.

Шаг 1. Найдите у себя дома или в фитнес-зале большое зеркало, или зеркальную стену (это нужно для того, чтобы оценить насколько правильно вы выполняете упражнение). Положив на пол коврик, примите упор лежа.

Шаг 2. Тело вытяните, опираясь на локти с предплечьями (согнув руки на 90 градусов) и на носки стоп. Локти должны быть строго под плечами. Руки напрягать не надо – они являются только опорной точкой. Чем ближе друг к другу стопы, тем тяжелее держать планку, и мышцы пресса напряжены сильнее. Раздвинув стопы, вы упростите выполнение упражнения.

Шаг 3. Спину надо держать плоской, как будто она прижата к стене. Мышцы брюшного пресса напрягаются, чтобы живот не провисал, а пятая точка вверх не выпячивалась. Удерживать равновесие легче, если напрячь мышцы ягодиц.

Шаг 4. В таком положении надо продержаться 30-60 секунд и выполнить от 3 до 5 повторов.

Дышать при выполнении упражнения надо правильно, ровно и спокойно, не задерживая дыхание. Длительное упражнение со статическим напряжением может повысить давление крови. Если у вас есть проблемы с сердцем, не делайте планку или проконсультируйтесь с врачом.

Начинать надо с небольшой длительности и старайтесь какждый следующий раз держаться как можно дольше. Чтобы увеличить время, можно придерживаться правил:

• делать упражнение по несколько раз в день, удерживая положение каждый раз дольше на несколько секунд;
• применять для укрепления профильных мускулов вспомогательные упражнения – подтягивания и отжимания;
• для укрепления мышц кора и низа спины помогут становая тяга и приседания.

Если у мышц живота недостаточно сил для выполнения классической планки, можно использовать вариант облегченный, согнув колени. Удерживая положение дольше двух минут, можно практиковать более продвинутые варианты упражнения. Делая планку, можно следить за временем или следить за своими ощущениями, прекращая повтор при появлении в животе ощущения жжения.

Чтобы запомнить как правильно выполнять планку приведем изображение:

Выполнять упражнение надо 3-4 раза в неделю, позволяя мышцам немного отдохнуть. Если удается легко простоять больше двух минут, можно упражнение усложнить.

История открытия

Формула Планка для теплового излучения

Основная статья: Формула Планка

Формула Планка — выражение для спектральной плотности мощности излучения абсолютно чёрного тела, которое было получено Максом Планком для равновесной плотности излучения u(ω,T){\displaystyle u(\omega ,T)}. Формула Планка была получена после того, как стало ясно, что формула Рэлея — Джинса удовлетворительно описывает излучение только в области длинных волн. В 1900 году Планк предложил формулу с постоянной (впоследствии названной постоянной Планка), которая хорошо согласовывалась с экспериментальными данными. При этом Планк полагал, что данная формула является всего лишь удачным математическим трюком, но не имеет физического смысла. То есть Планк не предполагал, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых связана с циклической частотой излучения выражением:

ε=ℏω.{\displaystyle \varepsilon =\hbar \omega .}

Коэффициент пропорциональности ħ впоследствии назвали постоянной Планка, ħ ≈ 1,054·10−34 Дж·с.

Фотоэффект

Основная статья: Фотоэффект

Фотоэффект — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.

Фотоэффект был объяснён в 1905 году Альбертом Эйнштейном (за что в 1921 году он, благодаря номинации шведского физика Озеена, получил Нобелевскую премию) на основе гипотезы Планка о квантовой природе света. В работе Эйнштейна содержалась важная новая гипотеза — если Планк предположил, что свет излучается только квантованными порциями, то Эйнштейн уже считал, что свет и существует только в виде квантованных порций. Из закона сохранения энергии, при представлении света в виде частиц (фотонов), следует формула Эйнштейна для фотоэффекта:

ℏω=Aout+mv22,{\displaystyle \hbar \omega =A_{out}+{\frac {mv^{2}}{2}},}

где Aout{\displaystyle A_{out}} — т. н. работа выхода (минимальная энергия, необходимая для удаления электрона из вещества), mv22{\displaystyle {\frac {mv^{2}}{2}}} — кинетическая энергия вылетающего электрона, ω{\displaystyle \omega } — частота падающего фотона с энергией ℏω,{\displaystyle \hbar \omega ,} ℏ{\displaystyle \hbar } — постоянная Планка. Из этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты, ниже которой энергии фотона уже недостаточно для того, чтобы «выбить» электрон из тела. Суть формулы заключается в том, что энергия фотона расходуется на ионизацию атома вещества, то есть на работу, необходимую для «вырывания» электрона, а остаток переходит в кинетическую энергию электрона.

Увеличение числа констант

Джеймс МаксвеллДжордж СтониМакс ПланкГилберт Льюисизвестны с одинаковой точностьюvv₁₀vvGГенри КавендишG.еженедельные комментарии в Natureсезонной зависимостиGBig G ChallengeЛеви Леблондаещеэта статьявот этаДаффа-Окуня-Венецианотема бурно обсуждаетсяэту статьюlattice reductionМауриц Корнелис ЭшерАльбрехта Дюрерасα–hβ-Gγαγβγγ.сα · hβ · Gγквантово-скорректированной силы притяженияс,hGфотон-фотонного рассеянияАнналы физикиGhh/k_Bформула Бекаполученную доном Пэйджем(брахиозаврзавропосейдонПресс, Лайтман, Пайерлс и Голдстатьиработа Барроуса и Острайкераидея базирования единиц на свойствах микроскопических объектов получала все большее распространениеиз-за различий в гравитационном потенциалеF = m аWolfram Open CloudМеждународным бюро мер и весовЭдгарустарая статьясколько пространственных измерений есть в нашей вселеннойс2(εμПолем Диракомαе₂ħсαтонкую настройкуальтернативные значениякомбинации константеще несколькоSpringerМера за меруNatureC,Ghhкотами ШредингераТомпкинса

Переход к формулам Рэлея — Джинса

Формула Планка точно согласуется с экспериментальными данными во всём интервале частот от 0 до ∞{\displaystyle \infty }. При малых частотах (больших длинах волн), когда ℏωkT≪1{\displaystyle {\hbar \omega \over kT}\ll 1}, можно разложить экспоненту по ℏωkT{\displaystyle {\hbar \omega \over kT}}. В результате получим, что

exp(ℏωkT)−1≈1+ℏωkT−1=ℏωkT,{\displaystyle \mathrm {exp} \left({\hbar \omega \over kT}\right)-1\approx 1+{\hbar \omega \over kT}-1={\hbar \omega \over kT},}

тогда и переходят в формулу Рэлея — Джинса.

uω(ω,T)=kTω2π2c3,{\displaystyle u_{\omega }(\omega ,T)=kT{\frac {\omega ^{2}}{\pi ^{2}c^{3}}},} и

Bω(ω,T)=kTω24π2c2.{\displaystyle B_{\omega }(\omega ,T)=kT{\frac {\omega ^{2}}{4\pi ^{2}c^{2}}}.}

Примечания

1. .
2. ↑ , с. 117.
3. .
4. , с. 402.
5. , с. 265.
6. , с. 226–227.
7. .
8. ↑ , с. 143.
9. , с. 10, примечание 6.
10. , с. 67.
11. , с. 41.
12. Простой называют , представляющую собой однородную изотропную среду (фазу) неизменного химического состава и массы, описываемую посредством переменных p{\displaystyle p} (давление), V{\displaystyle V} (объём) и T{\displaystyle T} (температура). Такая система обладает двумя термодинамическими степенями свободы, т. е. только два параметра состояния из трёх перечисленных являются независимыми. К простым системам относятся, в частности, газы и жидкости (флюиды) в ситуации, когда поверхностными эффектами и наличием внешних силовых полей можно пренебречь.
13. ↑ , с. 102.
14. Изоэнтропический (изоэнтропийный) — относящийся к системе с постоянной энтропией или процессу, протекающему без изменения энтропии; обмен веществом допускается.
15. , с. 103.
16. , с. 62–63.
17. Мысленное допустимое (не противоречащее условиям существования системы) изменение внутренней энергии. Встречающееся в литературе определение вариации как отклонения от равновесия, допускаемого наложенными на систему связями (условиями), означает то же самое.
18. , с. 78.
19. , с. 243–244.
20. ↑ , с. 126.
21. Для систем переменного состава дополнительно требуется равенство химических потенциалов её компонентов как условие выполнения химического равновесия.
22. , с. 146.
23. , с. 85–89.
24. , с. 112.
25. , с. 141.
26. , с. 312.
27. , с. 267.
28. , с. 12.
29. , с. 102.
30. , с. 457, примечание 12; с. 461–462, примечание 14.
31. , p. 194–235.
32. .
33. .
34. , с. 54–79.
35. , с. 61.
36. , с. 457, примечание 12.
37. «Планк… упорно не желал пользоваться методами Гиббса во всех изданиях своей «Термодинамики». Благодаря этому его изложение является довольно непоследовательным, поскольку он использует для нахождения условий термодинамического равновесия то энтропию, то свободную энергию, то вторую функцию Масье (полный термодинамический потенциал z, делённый на температуру, со знаком минус). Планк никогда не пользуется химическим потенциалом. «Термодинамика» Планка имела среди физиков почти такое же распространение, как «Теоретическая химия» Нернста среди физико-химиков, благодаря чему пользование «функцией Планка» (то-есть второй функцией Масье) получило широкое распространение». Семенченко В. К. Джосиа Виллард Гиббс, с. 21.

Переход к закону смещения Вина

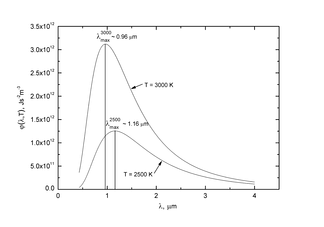
Для нахождения закона, по которому происходит смещение максимума φ(λ,Т) в зависимости от температуры, надо исследовать функцию φ(λ,Т) на максимум.

Для перехода к закону Вина, необходимо продифференцировать выражение по λ{\displaystyle \lambda } и приравнять нулю (поиск экстремума)

duλ(λ,T)dλ=4π2ℏc2{hckTλexp(hckTλ)−5exp(hckTλ)−1}λ6exp(hckTλ)−12={\displaystyle {\frac {\mathrm {d} u_{\lambda }(\lambda ,T)}{\mathrm {d} \lambda }}={\frac {4\pi ^{2}\hbar c^{2}\left\{{\frac {hc}{kT\lambda }}\mathrm {exp} \left({\frac {hc}{kT\lambda }}\right)-5\left\right\}}{\lambda ^{6}\left^{2}}}=0.}

Значение λm{\displaystyle \lambda _{m}}, при котором функция достигает максимума, обращает в нуль выражение, стоящее в фигурных скобках. Обозначив 2πℏckTλm=y{\displaystyle {\frac {2\pi \hbar c}{kT\lambda _{m}}}=y}, получим уравнение:

yey−5(ey−1)={\displaystyle ye^{y}-5(e^{y}-1)=0.}

Решение такого уравнения даёт y=4,96511…{\displaystyle y=4,96511\dots }. Следовательно,

Tλm=2πℏcyk=b.{\displaystyle T\lambda _{m}={\frac {2\pi \hbar c}{yk}}=b.}

Численная подстановка констант даёт значение для b=,0028777…{\displaystyle b=0,0028777\dots } К·м, совпадающее с экспериментальным, а также удобную приближённую формулу: λmT≈3000{\displaystyle \lambda _{m}T\approx 3000} мкм·К. Так, солнечная поверхность имеет максимум интенсивности в зелёной области (0,5 мкм), что соответствует температуре около 6000 К.

В контексте

Главный вопрос, который сейчас беспокоит потенциальных покупателей строящегося жилья, – брать или погодить?

Если покупать — то когда? По новым или по старым правилам? Или плюнуть на все и купить на вторичном рынке, тем более что цены уже сравнялись. Вопросов много. А застройщики и посредники, словно мантру, твердят одно и то же: завтра будет дороже, таких интересных предложений больше не будет.

Первая страшилка — переход на эскроу, вслед за которым обещают рост цен на 10–15%. Да, наверное, цена вырастет, но вряд ли резко и сразу на 10–15%. В противном случае у застройщиков просто не будет продаж: конкуренция пока велика, и кто будет покупать жилье дороже, чем у конкурентов, работающих по старым правилам? Значит, рост будет постепенным и займет 2–3 года. Кроме того, у застройщиков есть запас проектов. Впрочем, это тоже маловероятно — что цена будет расти на все, но потихоньку, на 3–7% в год. Не поднимать цены застройщики тоже не могут, так как они потеряют потенциальную прибыль, продав квартиры дешевле возможного. Уже за прошедший год средний бюджет сделки вырос на 10% в Петербурге и на 15% — в Ленобласти.

«Таких интересных предложений больше не будет» — будут. Во–первых, застройщики только в Петербурге уже получили разрешений более чем на 20 млн м2 жилья. И найти 30–50–70 м2, устраивающих именно вас, можно будет при любом раскладе. Сейчас земля официально закончилась только на Крестовском острове, да и там могут найтись варианты.

Надо понимать, что с переходом на эскроу–счета с рынка строящегося жилья автоматически снимается премия за риск (достроят дом или не достроят) — тот дисконт, который делал стоимость будущего (еще не построенного) жилья меньше, чем на вторичном рынке. И дисконт этот был немаленький: в наиболее нестабильные времена он достигал 40–50%. Покупая квартиры по новым правилам, мы будем уверены, что или дом достроят, или деньги вернут. Исходя из этого и надо принимать решение: покупать сейчас (с риском) или подождать. Но какие компании не выдержат переходного периода — не знает никто.

Покупка на вторичном рынке лишена рисков несдачи объекта. Понятны инфраструктура, благоустройство, соседи, но и тут есть риски: вторичное жилье может иметь темное прошлое. Кроме того, покупая уже обжитую квартиру, надо понимать, что придется делать в ней ремонт — скорее всего капитальный и дорогой: потолки, полы, неровные стены, сколотый кафель.

Если квартирный вопрос не стоит остро и не хочется рисковать, то покупайте на вторичке или ждите жилья по новым правилам. Любите подешевле, но с риском — покупайте сейчас. Деньги ваши, и окончательное решение — за вами.

2.3.2 Закон Планка для АЧТ

Функция Планка для равновесного излучения
может быть записана в виде удельной интенсивности
в единичном интервале частот ([эрг/см/c/Гц/стер])

(2.26)

Чтобы перейти к удельной интенсивности в
единичном интервалу длин волн, воспользуемся законом сохранения
энергии

и связью . Находим

(2.27)

Функция Планка приведена на Рис.  ()

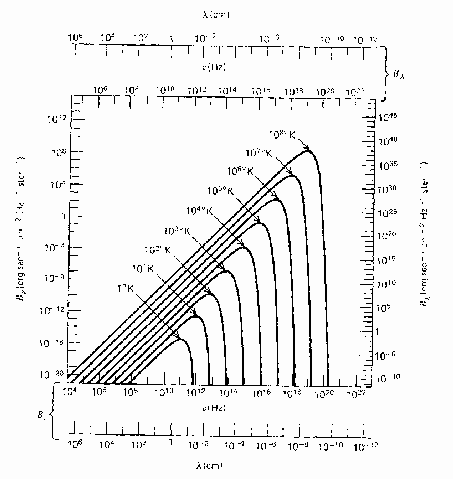Рис. 2.1 Спектр АЧТ

2.3.2.1 Предельные случаи и свойства функции Планка

Закон Рэлея-Джинса, ,

(2.28)

Обратим внимание, что в выражение
для интенсивности в этом случае
не вошла постоянная Планка, т.е. в этом пределе формула описывает
чисто классическое излучение

Попытка экстраполировать закон Рэлея-Джинса
в область более высоких частот приводит к расходимости,

(«ультрафиолетовая катастрофа»)

Закон Вина,

(2.29)

Монотонное изменение с температурой:

на всех . Это означает, что кривые функции
Планка для разных температур нигде не пересекаются друг с другом,
поанковская кривая с температурой целиком лежит выше кривой
с температурой .

Закон смещения Вина

Определим максимум в спектре АЧТ. Начнем с удельной интенсивности
на единичный интервал частот .

Максимум функции :

(2.30)

Подчеркнем, что
!!!

Закон Стефана-Больцмана

Полный поток энергии с площадки, излучающей как АЧТ,
пропорционален четвертой степени температуры.

(2.31)

где
эрг/см/c/град —
постоянная Стефана-Больцмана.

Плотность энергии и давление равновесного излучения

Плотность энергии АЧТ

(2.32)

или пользуясь результатом  ()

(2.33)

где

[эрг/см/град] — постоянная плотности излучения. Давление
равновесного излучения
 () при этом равно

(2.34)

Средняя энергия чернотельного фотона

По определению, это величина
, где
— плотность энергии, — плотность числа квантов.
Для АЧТ плотность энергии есть  (),

(2.35)

Делая замену переменных

в интегралах приходим к

(2.36)

Фермиевские интегралы в числителе и знаменателе сводятся к -функции
Римана
,
в приближении Вина это просто гамма-функции

.

Очень полезное приближение для плотности числа фотонов чернотельного
излучения получается с использованием приближения Вина:

2.2 Уравнение переноса
| Оглавление |
2.4 Характеристические темп… >>

Публикации с ключевыми словами: звезды — Межзвездная среда — Космология — теоретическая астрофизика — астрофизика Публикации со словами: звезды — Межзвездная среда — Космология — теоретическая астрофизика — астрофизика
См. также: Все публикации на ту же тему >>

Мнения читателей

Астрометрия
—
Астрономические инструменты
—
Астрономическое образование
—
Астрофизика
—
История астрономии
—
Космонавтика, исследование космоса
—
Любительская астрономия
—
Планеты и Солнечная система
—
Солнце

Итог

В стандартной модели Вселенной самая высокая из когда-либо зафиксированных температур была достигнута за доли секунды после Большого взрыва. В течение этого незначительного периода времени излучаемый свет имел длину волны 10 ^ -35 метров. Эта длина называется длиной Планка и является наименьшей измеримой длиной во Вселенной. Из-за этой небольшой длины волны температура достигала 1,416808·1032 кельвинов, или 142 квинтиллиона кельвинов (142 ниллионда по короткой шкале), что называется температурой Планка и является самым близким определением «абсолютной жары», которое мы имеем в настоящее время.

Помимо того, что температура Планка является самой высокой температурой, когда-либо теоретически достигнутой в нашей Вселенной, физики предполагают, что при любой температуре, превышающей стандарт Планка, гравитационные силы затронутых частиц станут настолько сильными, что они могут создать черную дыру. Черная дыра, которая создается из энергии, а не из материи, называется «кугельблиц». Наши общепринятые в настоящее время модели физики рушатся на фоне этого явления, оставляя многие вопросы без ответа.

Если вы что-то не поняли, предлагаем посмотреть этот ролик, из которого вы обязательно поймете многие вещи по этой теме:

https://youtube.com/watch?v=XEHbL3bnIbU

Вывод для абсолютно чёрного тела

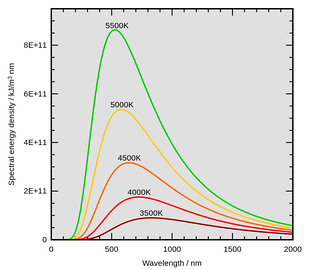Излучение абсолютно чёрного тела

Вследствие линейности уравнений электромагнитного поля, любое их решение может быть представлено в виде суперпозиции монохроматических волн; каждая — с определённой угловой частотой ω{\displaystyle \omega }. Энергия поля может быть представлена как сумма энергий соответствующих осцилляторов. Как известно из квантовой механики, энергия осциллятора принимает дискретные значения согласно следующей формуле:

En=ℏω(n+12).{\displaystyle E_{n}=\hbar \omega (n+1/2).}

Поскольку рассматривается равновесное излучение, то, используя каноническое распределение Гиббса, можно определить вероятность состояния осциллятора с заданной энергией:

Wn=1Z⋅exp(−EnkT).{\displaystyle W_{n}={1 \over Z}\cdot \mathrm {exp} \left(-{E_{n} \over kT}\right).}

Статистическая сумма Z{\displaystyle Z} равна:

Z=∑exp(−ℏωkT⋅(n+12))=exp(−ℏω2kT)⋅∑exp(−ℏωkT)n=exp(−ℏω2kT)1−exp(−ℏωkT).{\displaystyle Z=\sum \mathrm {exp} \left(-{\hbar \omega \over {kT}}\cdot (n+1/2)\right)=\mathrm {exp} \left(-{{\hbar \omega } \over {2kT}}\right)\cdot \sum \mathrm {exp} \left(-{{\hbar \omega } \over {kT}}\right)^{n}={\frac {\mathrm {exp} \left(-{{\hbar \omega } \over {2kT}}\right)}{1-\mathrm {exp} \left(-{{\hbar \omega } \over {kT}}\right)}}.}

Свободная энергия Ψ{\displaystyle \Psi } равна:

Ψ=−kT⋅ln⁡Z=ℏω2+kT⋅ln⁡(1−exp(−ℏωkT)).{\displaystyle \Psi =-kT\cdot \ln Z={\frac {\hbar \omega }{2}}+kT\cdot \ln \left(1-\mathrm {exp} \left(-{\hbar \omega \over kT}\right)\right).}

Для средней (математическое ожидание) энергии ε¯{\displaystyle {\overline {\varepsilon }}} воспользуемся уравнением Гиббса — Гельмгольца:

ε¯=∑(WnEn)=Ψ−(kT⋅∂(Ψ)∂(kT))=(kT)2⋅∂(ln⁡Z)∂(kT)=(kT)2⋅(ℏω2(kT)2+exp(−ℏωkT)⋅ℏω(kT)21−exp(−ℏωkT)){\displaystyle {\overline {\varepsilon }}=\sum (W_{n}E_{n})=\Psi -\left(kT\cdot {\frac {\partial (\Psi )}{\partial (kT)}}\right)=(kT)^{2}\cdot {\frac {\partial (\ln Z)}{\partial (kT)}}=(kT)^{2}\cdot \left({\frac {\hbar \omega }{2(kT)^{2}}}+{\frac {\mathrm {exp} \left(-{{\hbar \omega } \over {kT}}\right)\cdot {\hbar \omega \over (kT)^{2}}}{1-\mathrm {exp} \left(-{\hbar \omega \over kT}\right)}}\right)};

таким образом, средняя энергия ε¯{\displaystyle {\overline {\varepsilon }}}, приходящаяся на полевой осциллятор, равна:

ε¯=ℏω2+ℏωexp(ℏωkT)−1.{\displaystyle {\overline {\varepsilon }}={\frac {\hbar \omega }{2}}+{\frac {\hbar \omega }{\mathrm {exp} \left({\hbar \omega \over kT}\right)-1}}.},

(1)

Количество же стоячих волн в единице объёма в трёхмерном пространстве, в интервале (ω;ω+dω){\displaystyle (\omega ;\omega +d\omega )}, равно:

dnω=ω2dωπ2c3{\displaystyle \mathrm {d} n_{\omega }={\frac {\omega ^{2}\mathrm {d} \omega }{\pi ^{2}c^{3}}}}.

(2)

Следовательно, для спектральной плотности мощности электромагнитного излучения получаем:

uω()(ω,T)=ε¯dnωdω=ℏω32π2c3+ℏω3π2c3(exp(ℏωkT)−1),{\displaystyle u_{\omega }^{(0)}(\omega ,T)={\overline {\varepsilon }}{\frac {\mathrm {d} n_{\omega }}{\mathrm {d} \omega }}={\frac {\hbar {\omega }^{3}}{2\pi ^{2}c^{3}}}+{\frac {\hbar {\omega }^{3}}{\pi ^{2}c^{3}\left(\mathrm {exp} \left({\hbar \omega \over kT}\right)-1\right)}},}

где первое слагаемое связано с энергией нулевых колебаний, а второе — это и есть формула Планка.

Вывод, исходящий из распределения Бозе — Эйнштейна

Фотоны являются бозонами и подчиняются статистике Бозе — Эйнштейна. Для этой статистики, среднее число частиц с данной энергией ε{\displaystyle \varepsilon } равно:

n¯(ε)=1exp(εkT)−1.{\displaystyle {\overline {n}}(\varepsilon )={\frac {1}{\mathrm {exp} ({\varepsilon /kT})-1}}.}

По определению:

uε(ε,T)dε=εn¯(ε)dN(ε),{\displaystyle u_{\varepsilon }(\varepsilon ,T)\mathrm {d} \varepsilon =\varepsilon {\overline {n}}(\varepsilon )\mathrm {d} N(\varepsilon ),}

где dN=ε2dεπ2c3ℏ3{\displaystyle \mathrm {d} N={\frac {\varepsilon ^{2}\mathrm {d} \varepsilon }{\pi ^{2}c^{3}\hbar ^{3}}}} — число осцилляторов (в единице объёма) электромагнитного поля с данной энергией, в бесконечно малой окрестности ε=ℏω{\displaystyle \varepsilon =\hbar \omega }.

Подставив формулу среднего числа бозонов с данной энергией в эту формулу, получим для

uω(ω,T)=uε(ε,T)dεdω{\displaystyle u_{\omega }(\omega ,T)=u_{\varepsilon }(\varepsilon ,T){\frac {d\varepsilon }{d\omega }}}

формулу Планка.